Contactless LED Technology

In 2006, when the engineering team began developing an LED illumination system, the group considered the following limitations:

The LED modular illumination system generally used in commercial, architectural, residential or landscaping applications usually includes a DC power supply connected to 120 VAC (240 VAC). When modules do not have an integrated driver, the output of this power supply provides DC voltage to a supply rail, wire, or connectors providing electrical connection to LED arrays arranged in several illumination modules including ballast resistors (or current regulators). These modules are usually connected in parallel on a DC supply bus. The LEDs are connected with wires that are soldered permanently providing fixed electrical contacts. The LED illumination modules are connected to one another using two to four wires mechanically creating electrical contacts. In this conventional light circuit’s topology, the LED module uses a ballast resistor to provide a constant current to LEDs connected in series (since LEDs operate in current and not voltage). This dissipative method normally uses as much energy in the ballast resistor (dissipated energy) as in the LEDs, resulting in important losses of efficiency. This means there could be significant amounts of energy wasted in heat. Furthermore, the use of fixed electrical contact connectors can be prone to reliability troubles. For example, the exposure of the contact connectors to the surrounding atmosphere can cause contacts to deteriorate by chemical or electromechanical corrosion and fail prematurely. Over long distance, the illumination system comprising a power supply connected to an LED array provides non-uniform lighting since the voltage feeding the LEDs drops as a function of the distance between the LED array and the power supply.

In 2006, based on the above mentioned observations, the engineering team identified the need for an improved LED illumination system that would be reliable, simple and quick to install and that would operate at high frequency.

Basics of the Contactless LED Technology

The Contactless LED technology, such as HEICO lighting’s™ proprietary approach, is based on electromagnetic induction which is the production of energy across a conductor when it is exposed to a varying magnetic field as seen in figures 1 and 2.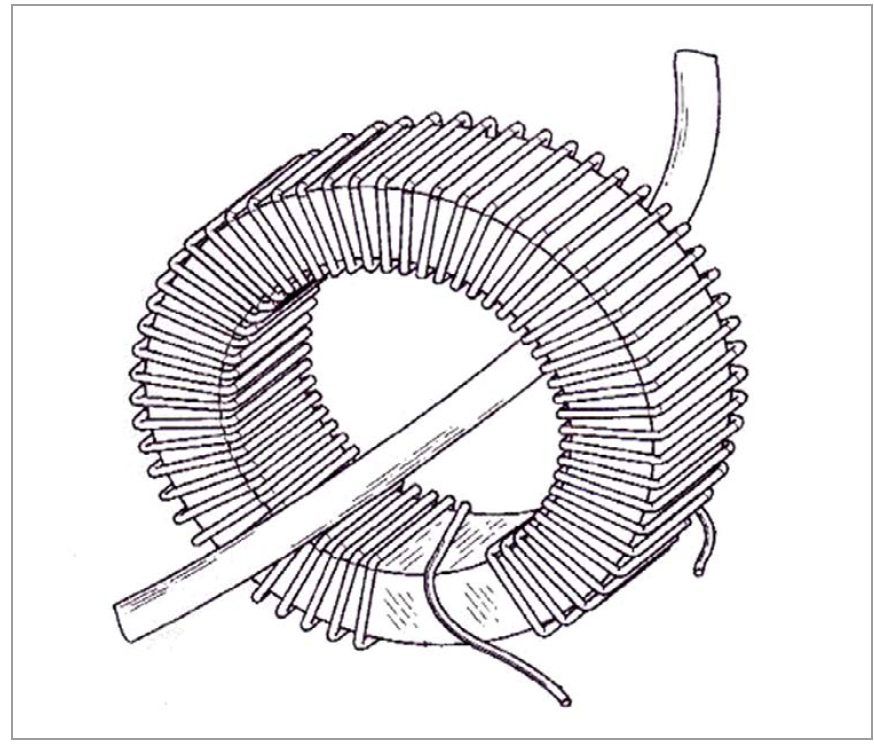

Figure 1 (left): Representation of the toroid ferrite - electromagnetic induction technology

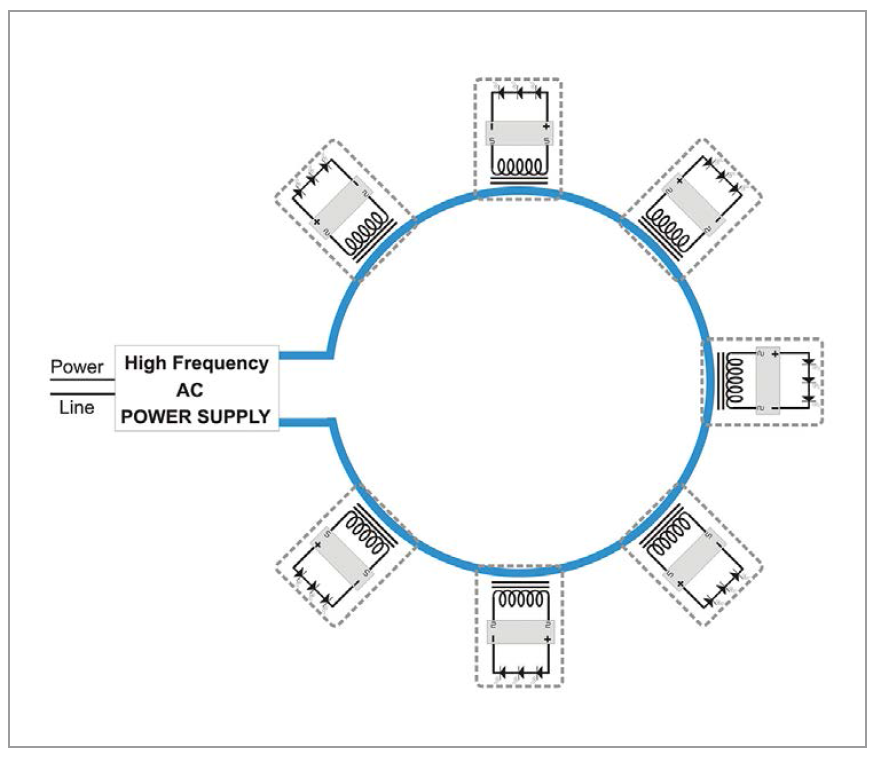Figure 2 (right): Contactless LED illumination system concept

The illumination system based on the Contactless LED technology comprises a power supply (AC current inverter) and a certain number of illumination modules including an electromagnetic coupling element and several lighting emitting diodes, wherein the electromagnetic coupling elements include a magnetic core arranged to receive output current from the power supply over a current-carrying loop forming a primary wire. The method includes positioning the primary wire in a close proximity to the illumination module without establishing an electrical connection, the positioning enabling inductive power transfer, as expressed in Faraday’s law, from the primary wire to a secondary wire connected to provide current to one or multiple LEDs.

“Contactless” means no connectors, soldering or crimping between the LED modules and their electrical conductor. The complete system is virtually connection-free and only requires two mechanical contacts at the output of the power supply as there is no need for any other contacts anywhere else in the system. The luminaires are driven without physical contact to the source!

The Power Supply Primary Side - Power Supply Features

The LED master power supply (LMPS) is constructed and arranged to transform the conventional 120 VAC to a high-frequency low-voltage electrical power provided to a primary wire forming a current carrying loop (the power supply output conductor).

All power supplies are Class 2 rated AC regulated current loop output Safety Extra Low Voltage (SELV) power supplies, but design options are similar to conventional power supplies. They may provide special features like the LMPS-750, which is an electrolytic capacitor free power supplies boasting a Mean Time Between Failure (MTBF) in excess of 50,000 hours, achieving a reliability matching that of LEDs. It is based on proprietary technology resulting in efficiency in excess of 95% as can be seen in figure 3.

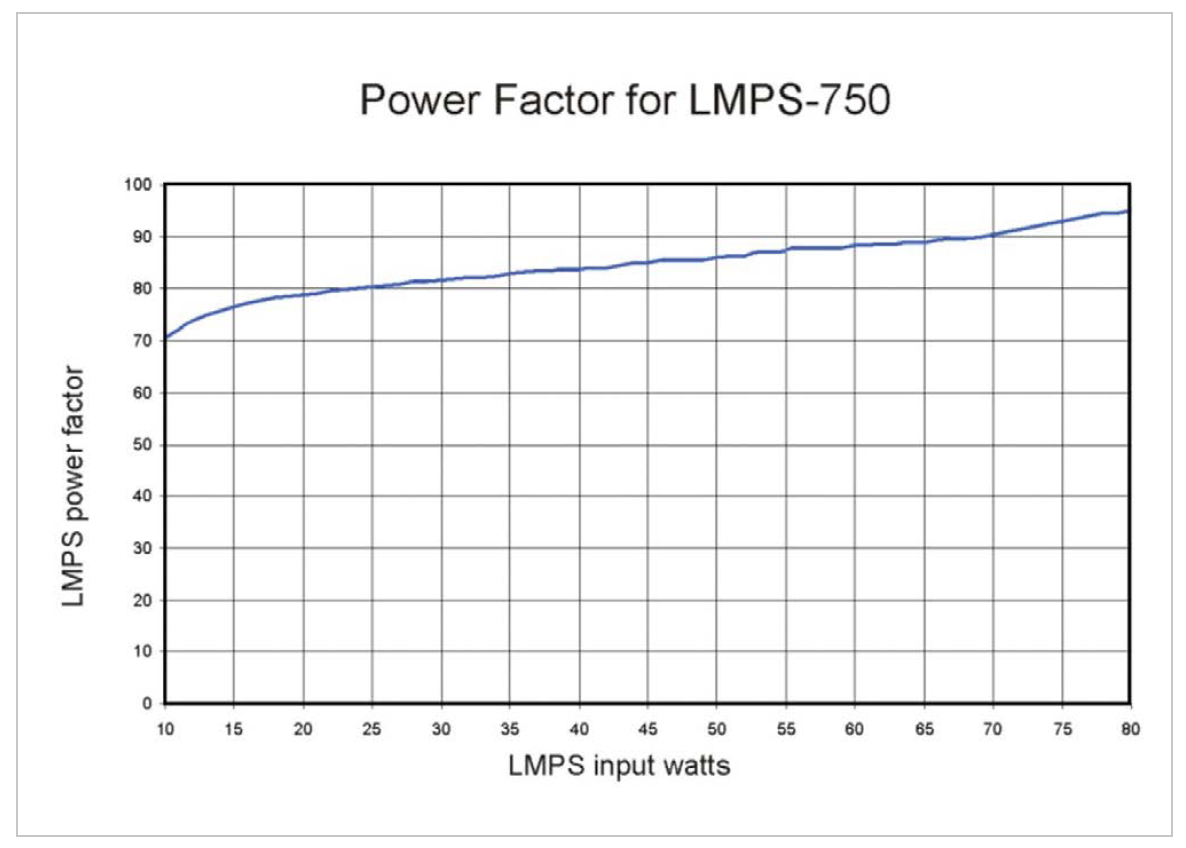Figure 3: Power factor for LMPS-750

“No shut-off” power supplies
All discussed power supplies are based on a regulated current loop. Their design provides a uniform illumination of all the LEDs that are connected to the power supply.

Should an overload situation occur, for example if the wrong number of LED modules is connected to the power supply, the power supply’s output current will simply be reduced automatically – the net result will be a reduction of the light intensity level and the power supply will not shut off, as can be seen in figure 4. The power supplies include an over-voltage or over-power detector. A transformer within the power supply senses the output voltage. When this voltage becomes excessive, because of overload, the main current regulating loop will be adjusted to meet Class 2 output limit and the output current will automatically be reduced to deal with overload.

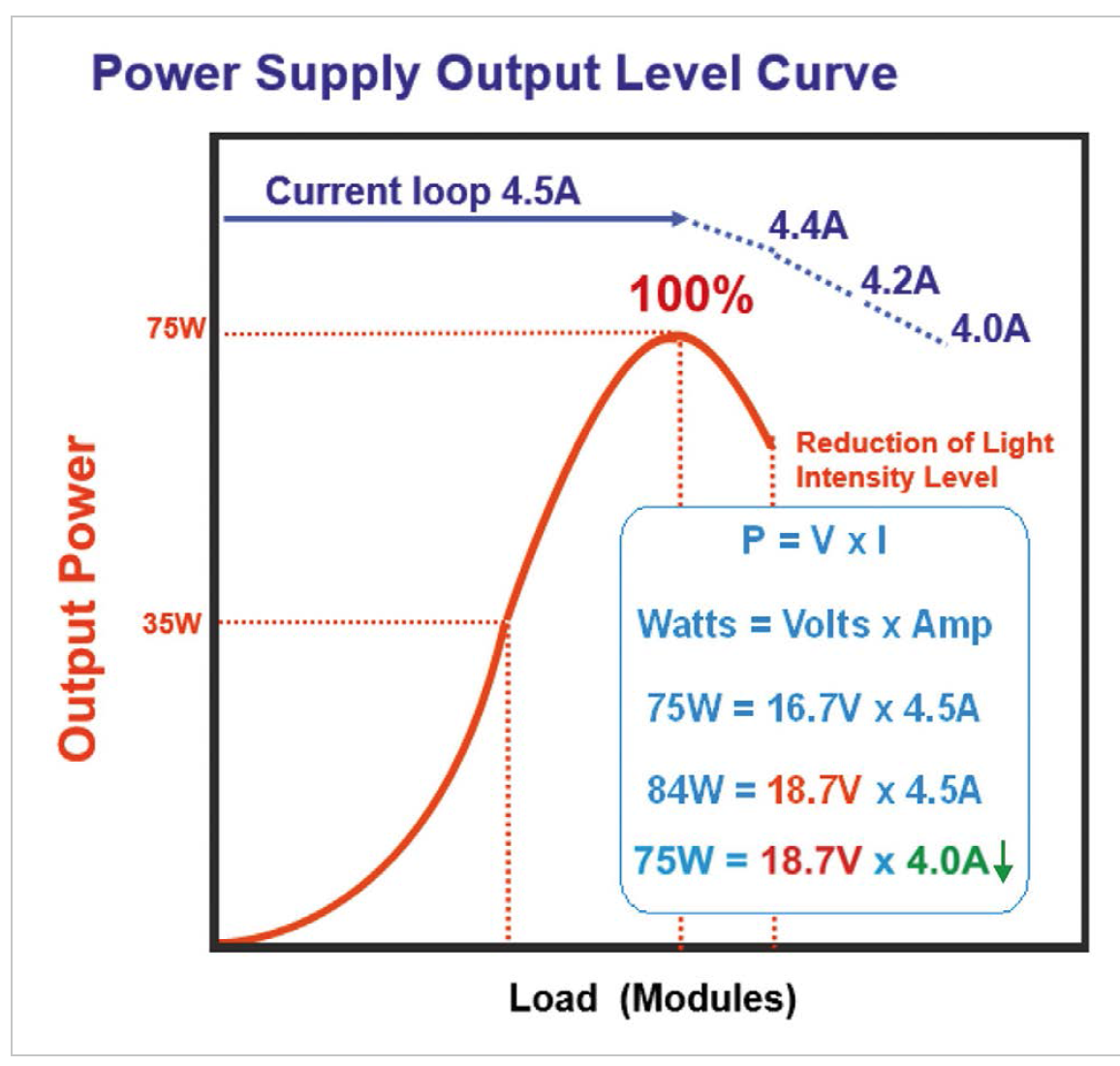Figure 4: “No shut-off” power supplies - output power behavior

The Power Supply Secondary Side – Module Features

Within the LED illumination module, a secondary wire is wound with on a magnetic core to enable inductive coupling from the primary wire, and provide current to several light emitting diodes.

There is no need to use a ballast resistor coupled to the LEDs, since the magnetic core winding generates a true current source. Indeed, the secondary current is equal to the primary current divided by a number of turns. One could compare this topology to a parallel system. The winding acts as a parallel system and divides the voltage induced by the primary wire in several secondary coils wound around the ferrite cores.

The current induced in the secondary wire of the transformer is rectified by a diode bridge to DC to drive an array of LEDs as can be seen in figure 5.

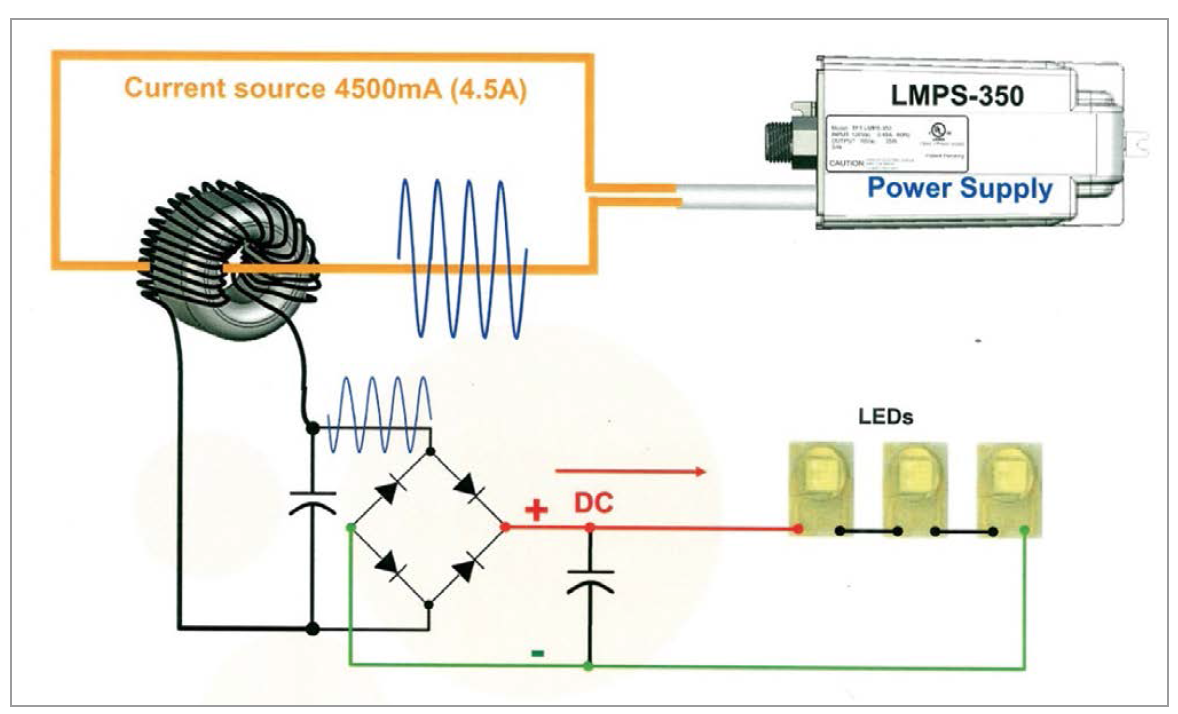Figure 5: Inside view of a contactless LED module

The magnetic core may have any shape. The primary wire is threaded through an opening in the core.

The power supplies may feed a variety of illumination modules that cater to the designer needs. Modules of any size, colour or light intensity can be installed simultaneously on the same power supply and do not need to remain in a fixed position. This can be accomplished since the power supplies are based on a constant current loop and each module has its own toroid ferrite that is designed to feed off the current loop.

Within the module body, the magnetic core and the secondary wire described above are encapsulated, thereby sealing the core and wire portion while enabling displacement of the primary wire with respect to the encapsulated magnetic core. The modules are IP67 rated; they are ideally suited for indoor and outdoor applications or for applications where reliability in a wet environment is required (Figure 6).

Figure 6: Installation in Langford fountain (Credit: Low Energy Lighting Technologies, EECOL Electric; Photo: The City of Langford)

A series of illumination modules may be controlled as a group by varying the current in the individual loops. This is achieved by employing a computerized control on each loop and allows the creation of different light effects.

Typical Configurations

There are a variety of configurations for the installation for this LED illumination system, here are two of the most typical ones:

Single wire loop with return:
Illumination modules are distributed on a long single wire and the wire comes back along the LED modules.

Twisted pair extension with single wire loop with return:
Modules are at the end of a twisted pair extension and distributed on a long single wire and the wire comes back along the modules.

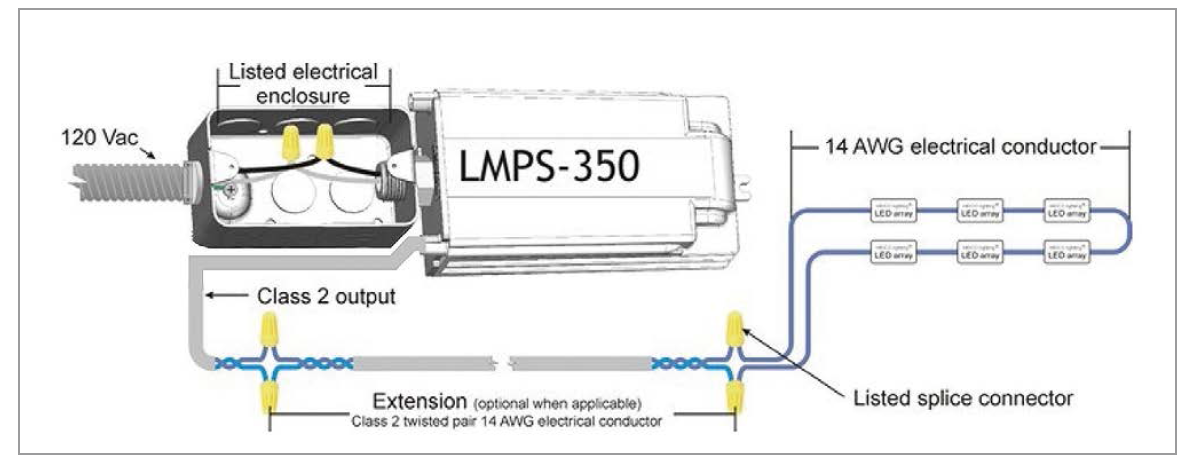Figure 7: Typical system diagram

Dimming

For dimming such a system, virtually any technology and protocol that is used in conventional installations is possible to control the dimmers. The LMPS-Dimmer Controller and a LMPS-Dimmer Extender (Figure 8) are built based on a proprietary technology.

Figure 8 (left): LMPS dimmer controller and LMPS dimmer extender

Figure 9 (right): Dimming method applied to the contactless LED illumination system

The Dimmer-Controller controls the LED illumination modules installed on the loop by using Pulse Width Modulation.

The Dimmer can be dimmed from 100% to 0% and can be controlled by any of the following methods:

• 0-10V

• PWM

• DMX protocol through a DMX Converter

• DALI protocol through a DALI Converter

Special Application Requirements: RGB Configuration – Case Study

Case study: Langford Fountain

Description of the project:
The City of Langford, in British Columbia, Canada, wanted to revitalize the Goldstream Avenue. They planned to build a fountain, in the center of the roundabout, and create beautiful animation of lights and water jets of various intensities that would be synchronized to music. The City of Langford collaborated with EECOL Electric and Low Energy Lighting Technologies (LELTEK) to achieve this creation that included 1440 Virgo™ XS Contactless LED modules.

Installation:
All LED modules are installed in series per colour. The loops are installed one over the other. The system is controlled by DMX protocol. Thus, all LMPS-350 power supplies are connected in series to the LMPS-Dimmer Controller and then to a 0-10V DMX converter. The LMPS-Dimmer controller is compatible with third party DMX controllers. Both (0-10 volts and PWM) external inputs are DMX512 compatible with the proper decoder.

Connection diagram:
As per the above connection diagram, the entire project has four loops of Contactless LED modules. Each loop is connected to an LMPS-Dimmer Controller which is connected to a DMX converter.

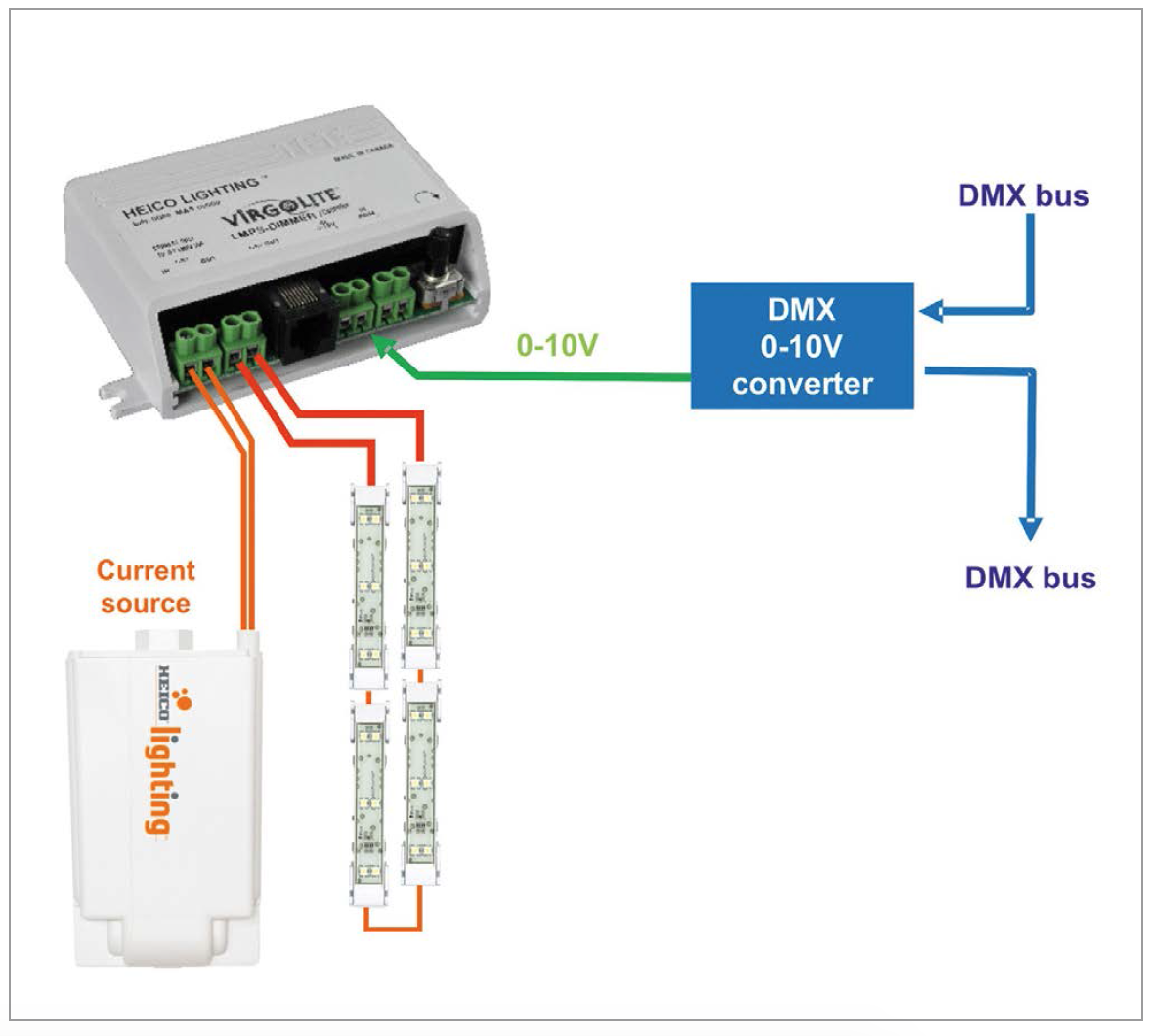Figure 10: Connection diagram of Langford Fountain RGB illumination concept

Advantages of an LED Illumination System Powered by Induction

The fact there is no need to establish electrical contact to any of the illumination modules results in increased reliability, lower cost, installation flexibility and extra safe operation.

The installation is very easy as there is only one wire used for powering the illumination modules and there is no polarity requirement since the technology is based on using alternative current provided by the master power supply. The power supplies have no shut off condition and their reliability matches that of the LEDs.

For outdoor applications, modules cannot corrode since there are no connections, hence no contact points that could corrode. In addition, the modules are encapsulated, further removing the risk of corrosion. In theory, a sinusoidal current (alternating current) affect the oxidation-reduction reaction (chemical reaction resulting in a transfer of electrons) causing corrosion by limiting the mass transfer of the substance in question to zero. In the case of a metal with DC current, several types of corrosions may occur such as atmospheric corrosion, chemical corrosion and galvanic corrosion. Thus, since only the AC portion of an LED system powered by induction is fully encapsulated and an oxidation reaction is not possible in this case (especially since there is no contact of the loop) it is chemically impossible to see the corrosion damage on this type of system.

A system of this aspect has also high efficiency (low power consumption).

System Efficiency

One of the key advantages of the Contactless LED technology is its efficiency at a very competitive price level.

The induction technology provides an extremely efficient usage of power since the only loss in the module circuitry is the one resulting from the rectification bridge in series with the LEDs. Inductive power transfer increases the efficiency of the module circuitry (which can be as high as 95% - depending on the selected LEDs) obtained from the input power for the light source to produce light.

The efficiency of the LED induction technology, coupled with the smart power supply design, yields an electrical efficiency in excess of 90% for the entire system

Under normal operating conditions, the efficacy of the LED modules varies from 75 lm/W to 110 lm/W depending on the colour and the intensity of the selected module.