Alternative Calculation Method Will Improve Thermal Analysis of LEDs - by Michiel Krüger, Ph.D. - Philips Lumileds

Up until now, thermal analysis of white LEDs has been an imperfect science. Too often LED lamp and luminaire manufacturers rely on insufficient, inaccurate or intangible data to determine the thermal performance of the LEDs in their applications, and, as a result, may over-engineer their heat sink design.

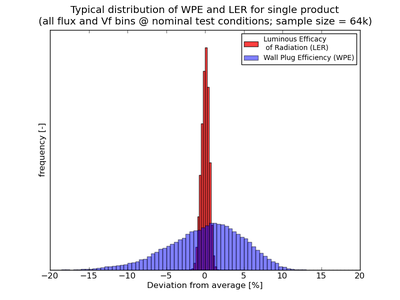
The industry’s most commonly used method of calculating how much power an LED converts into optical radiation, and how much heat is actually generated, is based on Wall Plug Efficiency (WPE). The trouble with WPE is that it can vary significantly between LED devices in the same product category, making it difficult for lamp and luminaire manufacturers to compare LED products. Furthermore, WPE is often a function of the operating conditions used. This paper provides a straightforward alternative to estimate the amount of heat generated by an LED based on Luminous Efficacy of Radiation (LER). LER for state-of-the-art, phosphor-converted white LEDs remains reasonably constant, enabling luminaire designers to use this metric to quickly approximate the amount of heat which is generated by an LED.

LEDs and heat dissipation

In thermal simulations, LEDs are at times modeled as simple resistive heaters—all the electrical power that goes into an LED is assumed to be converted into heat, which then, in turn, has to be dissipated from the luminaire. The problem with this assumption is that it is too conservative: high-brightness, phosphor-converted white LEDs now routinely convert 30% of the incoming electrical power into light while royal blue LEDs can reach conversion efficiencies well over 50%. Consequently, the total amount of power that has to be dissipated as heat from high brightness LEDs is often substantially less than the total electrical power that goes into the LEDs.

If this reduced heat-generating capacity is not properly accounted for in thermal simulations, the predicted temperatures in the resulting luminaire will be too high, and a more complex, more expensive heat-sink design will be required. This is especially important in those applications where a substantial amount of heat (5W-10W) has to be dissipated from a small PCB board and mechanically constrained heat sink, such as in retrofit LED light bulbs. To evaluate how the thermal performance of a lamp or luminaire stacks up, designers must properly account for what percentage of the incoming electrical power is converted into light and what percentage is converted into heat.

Currently, the LED industry often relies on a metric called Wall Plug Efficiency (WPE) to estimate the amount of heat generated by an LED. WPE is defined as the ratio of the total radiometric power emitted by the LED divided by the total electrical power going into the LED. Because WPE is dependent on the nominal flux and voltage of an LED and is a strong function of the actual drive current and junction temperature, it can vary significantly between LED devices in the same product category. It is therefore difficult to define a single “typical” WPE value that provides sufficient accuracy in thermal evaluations across different drive conditions, flux and voltage bin combinations for a specific LED product category.

Luminous Efficacy of Radiation

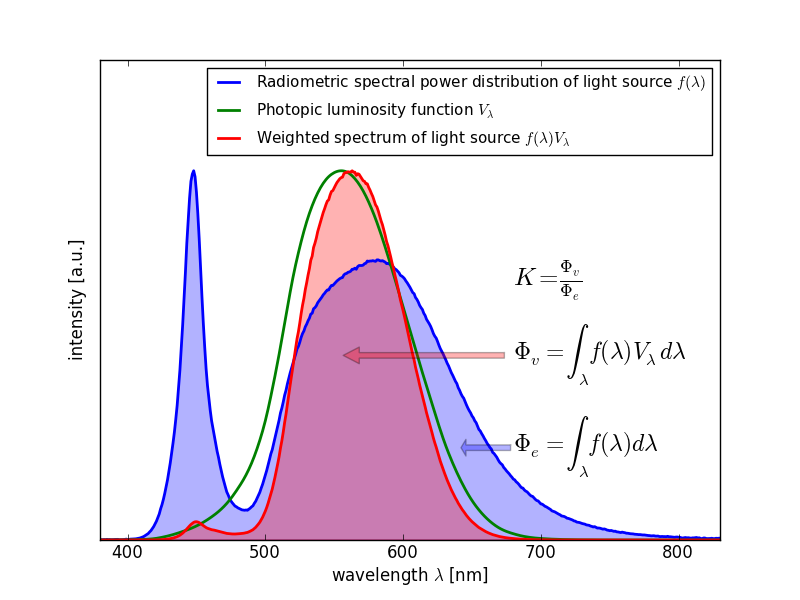
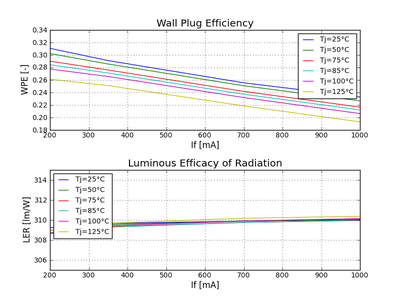
By comparison, Luminous Efficacy of Radiation (LER) is a compelling alternative to WPE when doing thermal evaluations of LED applications. Another LED performance metric, LER quantifies how well a light source produces visible light. More specifically, LER is defined as the total photopic luminous flux (in lumens) emitted by a light source divided by the total radiant power (in Watts) emitted by the same source. The LER value for an LED can be readily derived from the radiometric spectral power distribution, which is typically published in the LED datasheet (see Figure 1). Unlike WPE, LER does not vary substantially according to the nominal flux and voltage of an LED or the actual drive current and junction temperature (see Figure 2 and Figure 3). Once the value for LERis known, the total heat generated by an LED can be calculated as follows:

where "the rhombus sign" is the LER value for the LED under consideration,  is the LED drive current,  is the LED forward voltage at operating conditions, and  is the total luminous flux of the LED at operating conditions. For example, consider a phosphor-converted white LED with a typical LER value of 300lm/Wrad. Now assume that this LED is powered with a drive current of 1000mA, resulting in a luminous flux of 300lm and a forward voltage of 2.9V. According to the equation above, the total amount of heat generated by this LED is then 1.9W.

Since recent advancements in the production process of phosphor-converted white LEDs have enabled accurate color point control for LEDs within the same product category, LER values are much more consistent for LEDs within the same product family. In fact, leading manufacturers, such as Philips Lumileds, offer excellent color control for their latest illumination-grade LEDs (within a 3-step MacAdam ellipse). This allows manufacturers to define a typical LER value that is representative for all LEDs within the same product family, targeting a specific CCT.

The ONE Applications Team at Philips Lumileds now routinely uses LER values in its online “LED System Calculator.” This tool enables LED system designers to assess key performance metrics in their final lighting application, including how much heat their system will generate and how much light it will produce. As a result, Philips Lumileds makes it easier for designers to create lamps and luminaires that function as expected and to reduce costs associated with heat sinks. Moreover, LER makes it easier for them to compare LEDs in the same product category from different manufacturers, bringing additional clarity and ease to the LED specification process.

Author:
Michiel Krüger, Ph.D. - Philips Lumileds

Visit Philips Lumileds in the LED professional Buyer's Guide.